integral

Integración
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
Para otros usos de este término, véase INTEGRAL.
Para otros usos de este término, véase integración económica.

La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos.La integración es un concepto fundamental de las matemáticas avanzadas, especialmente en los campos del cálculo y del análisis matemático. Básicamente, una integral es una suma de infinitos sumandos, infinitamente pequeños.

Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la integral


es igual al área de la región del plano xy limitada entre la gráfica de f, el eje x, y las líneas verticales x = a y x = b, donde son negativas las áreas por debajo del eje x.

La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya derivada es la función dada f. En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.


La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos.

Aquí están las principales funciones primitivas:

Función : primitiva de función : derivada de

sumatorias y integrales

SUMATORIAS

1. Concepto de sumatoria.

A menudo resulta difícil trabajar con todos los elementos de una determinada sucesión, considerándolos como sumandos.
Para facilitar este trabajo se ha convenido representar la adición de los términos en forma abreviada mediante el signo S acompañado de la fórmula o término general que define a la sucesión y del rango de valores que tomará la variable considerada en esa fórmula.

Se denomina sumatoria de una sucesión an a la forma abreviada de escribir sus términos expresados como sumandos.
Se anota:
k=n
a1 + a2 + a3 + ... +an = S ak
k=1

2. Propiedades de las sumatorias.

a. Sumatoria de una constante.

Si c es una constante, entonces:

n
S c = n · c
k=1
Demostración:
n
Desarrollando la sumatoria S c , tenemos:
k=1
n
S c = c + c + c + ... + c (n veces)
k=1

por lo tanto, n
S c = n · c q.e.d.
k=1

b. Sumatoria de un producto de una constante por los términos de una sucesión.
Si c es una constante, entonces
n n
S c · ak = c · S ak
k=1 k=1
Demostración: n
Desarrollando la sumatoria S c · ak tenemos:
n k=1
S c · ak = c · a1 + c · a2 + ... + c · an
k=1
= c (a1 + a2 + ... + an )
n n
S c · ak = c · S ak q.e.d.
k=1 k=1

c. Sumatoria de la suma o resta de términos de dos o más sucesiones.
Si ak y bk son sucesiones, entonces se cumple que
n n n
S (ak + bk) = S ak + S bk
k=1 k=1 k=1
Demostración: n
Desarrollando la sumatoria S (ak + bk) tenemos:
k=1
n
S (ak + bk) = a1 + b1 + a2 + b2 + ... + an + bn
k=1
= (a1 + a2 + ... + an) + (b1 + b2 + ... + bn)
n n n
S (ak + bk) = S ak + S bk q.e.d
k=1 k=1 k=1


d. Descomposición de una Sumatoria en dos sumatorias.

n q n
S ak = S ak + S ak
k=1 k=1 k = q + 1




3. Propiedad telescópica de las sumatorias.

El desarrollo de algunas sumatorias tiene la particularidad de que casi todos sus términos se anulan, quedando éstas reducidas a solo dos términos.
Esta propiedad se denomina propiedad telescópica de las sumatorias.

Observemos los siguientes casos:
n
S (ak+1 - ak) = (a2 - a1) + (a3 - a2) + (a4 - a3) + ... + (an - an-1) + (an+1 - an)
k=1 n
de tal forma que: S (ak+1 - ak) = an+1 - a1
k=1
n
Análogamente: S (ak - ak+1) = a1 - an+1
k=1
La propiedad telescópica de las sumatorias también es válida para la sumatoria de los recíprocos de los términos vistos en los casos anteriores.
n n
S (1/ak + 1 - 1/ak) = 1/an + 1 - 1/a1 o S (1/ak - 1/ak + 1) = 1/a1 - 1/an + 1
k=1 k=1


La propiedad telescópica es de gran utilidad para hallar una expresión que permita calcular directamente el valor de alguna sumatoria o para demostrar si una sumatoria es igual a una expresión o fórmula dada, como veremos después en algunos ejemplos.

4. Sumatorias de una sucesión.

A veces es posible encontrar una fórmula o expresión general para la sumatoria de los términos de una sucesión, lo que, como veremos, simplifica notablemente el cálculo de dicha sumatoria.

A continuación, hallaremos una fórmula para algunas de las expresiones más usuales.

- Sumatoria de los n primeros números naturales.

Sea an = 1,2,3,4,5, ... , n - 1, n de modo que:
n
1 + 2 +3 + 4 + ... + (n - 1) + n = S k (1)
k=1
Conmutando los términos del primer miembro:
n
n + (n - 1) + (n - 2) + ... + 2 + 1 = S k (2)
k=1
Ahora, sumando miembro a miembro y término a término las sumatorias
(1) y (2) , obtenemos:
n
(n + 1) + (n + 1) + (n + 1) + ... + (n + 1) = 2 S k
__________________ n veces ___________________ k=1

Verificamos que el sumando (n + 1) se repite n veces; por lo tanto:
n
2 S k = n · (n + 1) / · 1/2
k=1
n
S k = n (n + 1) /2
k=1



- Sumatoria de los n primeros números naturales impares.

Sea 1,3,5,7,9, ... , (2n - 1) , de modo que:
n
1 + 3 + 5 + 7 + 9 + ... + (2n - 1) = S (2k - 1)
k=1

Aplicando propiedades de las sumatorias, obtenemos:
n n n n
S (2k - 1) = S 2k - S 1 = 2 S k - n
k=1 k=1 k=1 k=1
n
Por lo tanto: S (2k - 1) = n2
k=1

- Sumatoria de los cuadrados de los n primeros números naturales.

Sea 12, 22, 32 , 42 , ... , n2 , de modo que:
n
12 + 22 + 32 + 42 + ... + n2 = S k2
k=1
Para encontrar la fórmula o término general de esta sumatoria, es necesario utilizar sumatorias de números naturales elevados a una potencia mayor que 2 : en este caso, k3 y (k + 1)3.
n
De esta manera: 23 + 33 + 43 + ... + (n + 1)3 = S (k + 1)3 (1)
k=1

n
13 + 23 + 33 + ... + n3 = S k3 (2)
k=1
Si la sumatoria (1) le restamos término a término la sumatoria (2) , obtenemos:
n n
S (k + 1)3 - S k3 = (n + 1)3 - 1
k=1 k=1
n n
S (k3 + 3k2 + 3k + 1) - S k3 = (n + 1)3 - 1
k=1 k=1
n n n n n
S k3 + 3 S k2 + 3 S k + S 1 - S k3 = (n + 1)3 - 1
k=1 k=1 k=1 k=1 k=1
Aplicando las fórmulas ya conocidas, obtenemos:
n
3 S k2 + [3n (n + 1) 2] + n = (n + 1)3 - 1
k=1
Despejando:
n
3 S k2 = (n +1)3 - (n + 1) - [3n (n + 1) 2]
k=1
n
3 S k2 = (n +1) [(n + 1)2 - 1 - (3n 2)]
k=1
n
3 S k2 = (n +1) [n2 + n/2]
k=1
n
3 S k2 = n (n +1) [n + 1/2]
k=1
n
3 S k2 = n (n + 1) [(2n + 1) 2]
k=1
n
Finalmente, obtenemos: S k2 = n (n + 1)(2n + 1) 6
k=1



EJERCICIOS DE CONCEPTO DE SUMATORIA, PROPIEDADES, SUCESIONES Y APLICACIÓN DE FÓRMULAS.

Calcular las siguientes sumatorias:

50
1. S 4 = 4 + 4 + 4 + 4 + ... + 4 = 50 · 4 = 200
k=1 _______ 50 veces _______
5
2. S 3 (k2 + 1) = 3 S (k2 + 1) = 3 (2 + 5 + 10 + 17 + 26) = 3 · 60 = 180
k=1
6
3. S (k2 - 3k + 2) = S k2 - 3 S k + S 2
k=1
= (12 + 22 + ... + 62) - 3 (1 + 2 + ... + 6) + 6 · 2

= 91 - 3 · 21 + 12 = 40
5
4. S k (k + 1) 4 = 1/4 S (k2 + k) = 1/4[S k2 + S k]
k=1
= 1/4 [(1 + 4 + 9 + 16 + 25) + (1 + 2 + ... + 5)]
=1/4 [55 + 15] = 1/4 · 70 = 35/2

n
5. S 1/(k (k + 1)) = S (1 + k - k) k (k + 1) =
k=1
S [(k + 1) k (k + 1) - (k k (k + 1))] =
S [1/k - 1/(k + 1)] = 1 - 1/(n + 1) = (n + 1 - 1) (n + 1) = n/(n + 1)

n
S 1/(k (k + 1)) = n/(n + 1)
k=1

INTEGRAL DEFINIDA
Hay infinidad de funciones extraídas del mundo real (científico, económico...) para las cuales
tiene especial relevancia el área bajo su gráfica. Vamos a ocuparnos del cálculo de esas
áreas.
Área

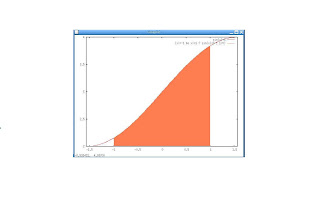
APROXIMACIÓN AL ÁREA BAJO UNA CURVA
Si conocemos la ecuación de una curva y = f(x) que toma valores no negativos, ¿cómo
calcularemos el área entre la curva, el eje X y dos abscisas, x = a y x = b?
Una idea útil consiste en dividir [a,b] en tramos y aproximar el área mediante rectángulos con
base en el eje X y altura el mínimo valor que toma la función en cada tramo.

Si el intervalo [a,b] se ha partido en n trozos, no necesariamente iguales:
a = x0 < xn =" b" i ="1" href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4aMRvPtNfk1CtLmHIfv2C0XboZqMcKmK5X1chSH45Qraf_dKWzqy3m00R7sfUdbQuU-0BrXDxeA0BqzQ_fThPZvV9hs68MjJQhFOYWVBFJirp-U-MpabH8AgBIaTMNcW5RkSyDf4x4pcr/s1600-h/Dibujo323.bmp">

¿Cómo aproximarnos más al valor del área que buscamos?
- Evidentemente, si tomamos unos rectángulos más finos, es decir, si los puntos xi los
tomamos cada uno más cerca del siguiente, tanto el área por defecto como el área por
exceso se aproximan más que antes al área del recinto.
– Y si, en vez de tomar el valor máximo o el mínimo de cada intervalo, tomamos un valor
intermedio, la aproximación podría ser mejor todavía.

INTEGRAL DE UNA FUNCIÓN CONTINUA
Sea f una función continua en [a,b] tal que f  x≥0 . Al área entre la gráfica de f, el eje X y
las abscisas x = a y x = b la llamaremos ∫a
b
f , que se lee integral entre a y b de f.
También se designa por ∫a
b
f  x  y por ∫a
b
f  xdx .
ÁREAS NEGATIVAS
Si consideramos que los recintos situados debajo del eje X tienen área negativa, entonces el
proceso anterior es válido para funciones cualesquiera, sin imponerles la condición de que
f  x≥0
Para funciones negativas, también el área por defecto queda debajo de la curva y el área por
exceso, encima de la curva, como puedes apreciar en las imágenes que siguen.

PROPIEDADES DE LA INTEGRAL
1.- ∫a
a
f  x  dx=0 cualquiera que sea f.
2.- Si f  x 0 y continua en [a , b] , entonces ∫a
b
f  x  dx0 ,
y si f  x 0 en todo [ a , b] , entonces ∫a
b
f  x  dx0 .
3.- Si abc y f es continua en [a , c] , entonces:
∫a
b
f  x  dx ∫b
c
f  x  dx= ∫a
c
f  x  dx
4.- ∫a
b
f  x  dx ∫a
b
g x  dx= ∫a
b
 f g x  dx
5.- c∫a
b
f  x  dx=∫a
b
c⋅f  x  dx cualquiera que sea el número c.
6.- Si para cada x∈[a , b] es f  x ≤g x  , entonces ∫a
b
f  x  dx≤∫a
b
g x  dx
7.- Si f es una función continua en [ a , b] , entonces existe un número c∈[a , b] tal que:
∫a
b
f  x  dx= f  c ⋅ b−a
Esta propiedad se llama teorema del valor medio del cálculo integral

Ejercicios
1.- Repasa los ejercicios de la sesión anterior para ilustrar con ejemplos las propiedades que
se relacionan arriba.
2.- Observa y contesta:
Observa que si f cambia de signo en [a , b] , la ∫a
b
f nos da la suma algebraica de las
áreas que están por encima y por debajo del eje X, cada una con su signo. Si
quisiéramos calcular el área en términos absolutos, tendríamos que calcular la
integral de cada recinto y, antes de sumar, cambiar de signo las negativas ¿no? ¿Qué
propiedad estamos utilizando?
CÁLCULO DE ÁREAS MEDIANTE INTEGRALES
Si para calcular el área comprendida entre una curva y= f  x  , el eje OX y las dos abcisas,
x=a y x=b , nos limitamos a calcular ∫a
b
f  x  , nos podemos encontrar en alguno de
estos casos:
Aquí,

Aquí, el resultado de la integral no representa el área buscada. Ello es debido a las
compensaciones que se producen de las partes positivas con las negativas.
La forma correcta de proceder será calcular, por separado, las integrales de los diversos
sectores y, posteriormente, sumar sus valores absolutos

Para calcular el área comprendida entre la curva y= f  x  , el eje OX y las abcisas x=a y
x=b , conviene dar los siguientes pasos:
I. Resolver la ecuación f  x =0 para averiguar los puntos de corte de la curva con
el eje X.
II. Seleccionar, de entre las raíces de la ecuación anterior, aquellas que estén
comprendidas entre a y b. Imaginemos que estas raíces, ordenadas de menor a
mayor, sean x1, x2 y x3. Es decir, se cumple: ax1x2x3b
III. Calcular ∫a
x1 f , ∫x1
x2 f , ò 3
2
x
x
f y ∫x3
b
f
Sus áreas son los valores absolutos de estas cantidades y el área buscada es la
suma de ellas.
Observemos que, con estos pasos, no es necesario dibujar la curva.
ÁREA COMPRENDIDA ENTRE DOS CURVAS
El área comprendida entre dos curvas, f y g, es igual al área comprendida entre la función
diferencia, f −g , y el eje OX.
Ejercicios resueltos
1.- Hallar el área comprendida entre la curva y=x3−x , el eje X y las rectas x=0
y x=2 .
Como ya sabemos, probablemente la integral ∫0
2  x3−x  dx no nos dará la solución correcta. Debemos
proceder así:
I. Hallamos las soluciones de la ecuación x3−x=0 . Son –1, 0, 1.
II. Ordenamos los extremos del intervalo y las raíces que haya entre ellos: 0, 1, 2.
III. Calculamos una aproximación al valor de las integrales con nuestra hoja de cálculo:
∫0
1
x3−x=−0.25 y ∫1
2
x3−x=2.25 aproximadamente
IV. Una aproximación al área buscada es la suma de los valores absolutos de estas aproximaciones